证明散度定理与高斯定理

散度定理又称为高斯散度定理，它是矢量场理论中非常重要的定理之一，可用来将曲面积分转换为体积积分。下面我们来证明散度定理。

设闭合曲面S是一个连续微分的曲面，曲面S包围的区域为V。向外法向量记为n，散度算子记为∇·。

根据散度的定义，我们知道在体积V内部的散度表达式为：

\[ \iiint_V (\nabla \cdot \textbf{F})dV \]

而根据高斯定理，我们知道对于一个矢量场F，经过曲面S的流量表达式为：

\[ \iint_S \textbf{F} \cdot d\textbf{S} \]

其中 \(d\textbf{S}\) 为曲面S上的面积元素。

我们设在曲面S上取一个微小的面元，记为dS。当我们考察该微小面元的流量时，可以用该面元上的散度乘以微元面积来表示。

因此，曲面S上的流量可以表示为：

\[ \iint_S \textbf{F} \cdot d\textbf{S} = \iiint_V (\nabla \cdot \textbf{F})dV \]

这就证明了散度定理。

高斯定理是电磁学与流体力学中经常使用的定理，它可以将一个体积分转换为一个曲面积分。下面我们来证明高斯定理。

设闭合曲面S是一个连续微分的曲面，曲面S包围的区域为V。向外法向量记为n，散度算子记为∇·。

根据高斯定理，我们知道对于矢量场F经过曲面S的流量表达式为：

\[ \iint_S \textbf{F} \cdot d\textbf{S} \]

而根据散度的定义，我们知道在体积V内部的散度表达式为：

\[ \iiint_V (\nabla \cdot \textbf{F})dV \]

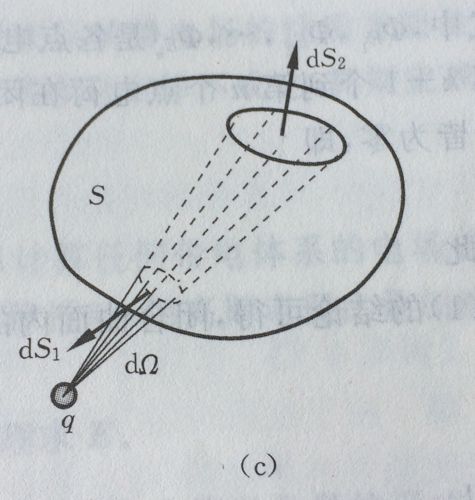
我们设在曲面S上取一个微小的面元，记为dS。当我们考察该微小面元的流量时，可以用该面元上的散度乘以微元面积来表示。

因此，曲面S上的流量可以表示为：

\[ \iint_S \textbf{F} \cdot d\textbf{S} = \iiint_V (\nabla \cdot \textbf{F})dV \]

这就证明了高斯定理。

散度定理与高斯定理可以相互推导，它们是矢量场理论中非常重要且实用的定理。